Logique Mathématique et Fondement
des Mathématiques
Jérôme Legras
Copyright © Jérôme Legras.
L'auteur donne ici permission
d'utiliser cet article sous forme électronique seulement, en partie
ou en totalié, à toute personne ou institution pour des motifs
éducatifs, tant qu'aucun payement n'est perçu en retour.
Introduction
Les méthodes mathématiques ont connu
un grand bouleversement à partir du XIXème siècle.
Une volonté de rigueur, de 'perfection' dans la formulation
des mathématiques est apparue. Certains auteurs espéraient
même parvenir à développer un système
global qui parviendrait à rendre compte de toutes les mathématiques
existantes et potentielles (Programme de Hilbert). Une composante
essentielle de cette marche vers la rigueur est la logique mathématique
avec son cortège d'axiomes, de lois, de conséquence
valide, etc. Il semble donc qu'une première définition
(intensionnelle) de la logique mathématique peut être:
l'ensemble des règles de déduction que l'on utilise
en mathématiques. Hélas la situation est bien plus
complexe, comme les mathématiciens du XIXème ont
bien vite pu s'en rendre compte.
Pour faire de la logique mathématique, c'est
à dire pour tenter de préciser quelles sont les
conséquences valides et les déductions acceptables
en mathématiques, il faut disposer d'un langage dans lequel
exprimer cette théorie. Ce langage ne peut être cette
même logique, puisque l'on cherche justement à la
comprendre. Il ne peut pas non plus être les mathématiques,
puisque l'on cherche à préciser le fonctionnement
des mathématiques. Il faut donc inventer un nouveau langage
(qui cherchera lui aussi à être rigoureux, mais dans
quel sens ?), que l'on appelle la théorie de la
démonstration. Mais à nouveau ce langage doit
être étudiée dans un autre langage, etc. Cette
régression infinie de métalangages (langage
à propos de langages) rend illusoire l'idée d'une
formalisation aboutie, définitive des mathématiques,
et renvoie au concept de mots non-définis Korzybskien,
en le poussant à l'extrême: à un certain stade
le mathématicien devra avoir un langage non-défini,
ce que l'on appelle le domaine intuitif de base.
Si l'on veut bien accepter de nommer mathématiques
l'ensemble de ces langages, on peut convenir d'appeler logique
mathématique, la logique traitée par les méthodes
mathématiques. Il y a cependant là une imprécision,
puisque la logique mathématique est également la
logique utilisée en mathématiques.
Toute œuvre mathématique fait appel à la logique,
et la logique se fait à l'aide des méthodes mathématiques.
Cette situation est très semblable au vieux paradoxe grec,
dit paradoxe du menteur, ou encore au paradoxe que Russell a rendu
célèbre sous le nom de " paradoxe du barbier ".
Pour n'en citer qu'une version simple, considérons la phrase
" Je mens toujours ". L'auteur de cette phrase
ment-il ou dit-il la vérité ? Toutes les variantes
de ces paradoxes se fondent sur l'autoréférence,
et se résolvent à l'aide de métalangages.
Il en va de même en logique mathématique: en scindant
les mathématiques en de multiples métalangages on
parvient à isoler chacun d'entre eux et à l'étudier
sainement.
Dans le cadre de la logique mathématique il
est intéressant de préciser cette notion de métalangage,
en essayant de la visualiser. On peut, comme le décrit
S. C. Kleene dans son introduction à la logique mathématique:
imaginer que l'on place la logique que l'on veut étudier
dans une boite, et on l'étudie à l'aide d'une autre
logique, placée dans une autre boîte. Puisque la
logique est avant tout une affaire de grammaire, c'est-à-dire
de construction de phrases correctes (et non de vocabulaire),
on appelle le contenu de ces 'boîtes' des langages. Le langage
étudié est le langage objet, et la logique
que nous utilisons pour l'étudier est le langage de
l'observateur. Il est vital de comprendre que l'étude
de la logique ne peut se faire qu'au sein d'une autre logique
— qu'elle même on pourra étudier éventuellement
au sein d'une autre troisième logique, etc. — et non pas
ex-nihilo. Ce point essentiel est parfois dur à admettre,
de même qu'on a parfois du mal à admettre que certains
des mots que l'on utilise tous les jours sont des mots non définis.
Kleene est très explicite à ce sujet puisqu'il dit
" A quiconque s'y refuserait [à garder cette
distinction présente à l'esprit], nous suggérons
de fermer le livre dès maintenant et de se chercher un
autre centre d'intérêt, par exemple l'acrostiche
ou l'élevage d'abeilles ".
On conçoit dès lors qu'il existe plusieurs
logiques, et autant de métalangages pour les étudier,
qui diffèrent par le contenu des axiomes, ou par la forme
même de la grammaire. On peut citer le calcul des prédicats,
le calcul propositionnel, etc. Nous allons choisir d'en
étudier une plus particulièrement, que l'on pourrait
appeler fondement des mathématiques, ou arithmétique
formelle, à la fois pour son caractère capital en
mathématiques, mais aussi pour les importants résultats
qui en ont découlé (Théorème de Godel
notamment). Auparavant, il va nous falloir préciser le
sens de la démarche axiomatique et donner quelques notions
de calcul propositionnel et de calcul de prédicats.
Axiome et intuition en mathématiques
Avant d'en venir à décrire les fondements
'classiques' des mathématiques et les principales formes
de logique, nous allons un peu détailler la méthode
axiomatique et le 'sens' à accorder aux différentes
formulations de la logique. La méthode axiomatique domine
largement les mathématiques depuis le milieu du XXème
siècle. On considère même que toutes les mathématiques
standards sont décrites par un système d'axiomes
assez concis, le système Zermelo-Frankel-Choix. Il faut
noter que la méthode axiomatique peut s'appliquer à
des sous ensembles des mathématiques; et que la pratique
mathématique veut que chaque nouvel objet introduit le
soit axiomatiquement.
Le fonctionnement de la méthode est le suivant:
on se propose de partir de termes primitifs, appartenant
à ce que l'on nomme le domaine intuitif de base. Ces termes
sont définis grossièrement, afin de donner une idée
intuitive de leurs propriétés, mais ce sont essentiellement
des mots non-définis. En général, ils reposent
sur des abstractions de bas niveau et faciles à appréhender,
telles que l'existence, l'appartenance, la négation, la
notion d'ensemble, etc. Sur la base des propriétés
intuitives que l'on accorde à ces termes primitifs, on
formule ensuite des axiomes ou postulats. La pensée intuitionniste
(voir plus loin) souligne que ces postulats doivent être
en accord avec des observations possibles (en écartant
notamment les cas infinis puisqu'invérifiables), alors
que la pensée classique est beaucoup plus flexible à
ce sujet, et ne s'intéresse qu'aux conséquences
qui découlent des postulats, sans se poser réellement
de question sur un éventuel contenu des postulats. Enfin,
à l'aide de la logique mathématiques, des axiomes,
et de nouvelles définitions formées à partir
des termes primitifs, on trouve des théorèmes.
Ces théorèmes doivent découler des axiomes
de manière essentiellement mécanique, et le résultat
obtenu est indépendant de celui qui le trouve, des ses
interprétations, etc. Cette démarche mécanique
permet de valider une idée, et d'affirmer 'positivement'
si un résultat découle des axiomes choisis ou non.
Il faut noter que cette méthode axiomatique
est une version rigoureuse et formalisée de ce que chacun
réalise tous les jours, et ce quasiment en permanence.
Nous effectuons régulièrement, de manière
très souvent inconsciente et chaotique, des déductions
à partir de nos prémisses et de nos termes non définis.
Ce sont ces déductions qui déterminent notre façon
de voir le monde, de l'appréhender, etc. En cela la méthode
axiomatique est très 'naturelle', et se contente de pousser
à un degré de formalisation et de rigueur plus élevé
un mécanisme profondément humain. Pour plus de détails
sur nos prémisses et termes non définis, reportez-vous
à Science and Sanity (of course).
Les deux systèmes axiomatiques les plus célèbres
sont ceux d'Euclide et de Frankel. Euclide visait à décrire
la géométrie spatiale, et ses axiomes ont traversé
les siècles. Ceux de Frankel (1922-1961) sont plus récents
et appartiennent aux fondements des mathématiques: ils
décrivent la notion d'ensemble, et formulent les premières
propriétés ainsi que les conditions d'existence
de ces ensembles. Deux des axiomes de Frankel sont très
liés à la sémantique général,
puisqu'il s'agit des axiomes stipulant qu'on peut définir
un ensemble par intension (en donnant une propriété
caractéristique), ou par extension (en énonçant
les éléments un à un).
Revenons un instant sur l'opposition entre intuitionniste
et classique que nous avons évoquée plus haut. Lorsqu'un
mathématicien réfléchit, cherche à
résoudre un problème, etc., il a en général
deux méthodes de travail qui s'offrent à lui. La
première consiste à essayer de visualiser physiquement
la situation, et d'en intuiter la solution à l'aide de
son intuition géométrique, de son sens physique,
etc. Les mathématiciens ont une expression très
éloquente à ce sujet, ils disent chercher " ce
qui fait que ça marche ", alors que tous savent
très bien que c'est l'ensemble des axiomes, lois, règles
logiques de déduction, etc., qui " font que ça
marche ". On est là dans le domaine intuitionniste.
Mais il arrive que l'on ne 'voie' rien. Il faut alors poser clairement
les axiomes dont on dispose, et mécaniquement chercher
la suite de conséquences valides qui mènera au résultat,
sans vraiment comprendre intuitivement l'interprétation
physique du travail mené. On est là dans le domaine
classique, ou moderne. Rentrons un peu dans les détails
de ces deux écoles.
La démarche moderne ne cherche plus à
accorder de 'sens primitif' aux termes primitifs et se contente
de poser les axiomes et d'en déduire les théorèmes,
plus à même de conduire à des interprétations
physiques. Cette méthodologie a soulevé de nombreuses
critiques, notamment sur le choix des axiomes. Comment déterminer
les axiomes intéressants, si on refuse d'accorder un sens
intuitif aux termes primitifs ? Comment choisir si un axiome
est meilleur si on ne sait pas ce qu'il signifie ? Au vu
des résultats, répondent certains, mais on ne connaît
pas les résultats qu'auraient donné d'autres axiomes !
La pensée 'intuitionniste' propose de donner une interprétation
physique dès le niveau des axiomes, et de tenter de formuler
des énoncés que l'on pense physiquement vrais, évitant
ainsi ce que Kleene appelle le nihilisme mathématique:
une construction stérile ne parlant pas de notre expérience
physique quotidienne. Le débat entre intuitionniste et
axiomatique standard est loin d'être clos, et il n'est pas
question de rentrer ici dans les détails. Disons simplement
que les intuitionnistes refusent la construction d'objets mathématiques
à partir de simples axiomes, de mots, et proposent de se
contenter de procédés mécaniques. L'existence
même des entiers naturels est au cœur du débat.
Les intuitionnistes, notamment Brower, furent les premiers à
critiquer la loi du tiers exclu: valable dans un ensemble fini,
elle est caduque dans le cas infini, puisqu'il est humainement
impossible de vérifier pour chaque élément
de l'ensemble infini s'il vérifie une propriété
donnée ou non. La question la plus 'saine' qu'un tel débat
suggère, " Quelles sont les mathématiques
les plus utiles, formalistes ou intuitionnistes ? "
n'a jamais vraiment été résolue ou même
traitée correctement. Il est fort probable que les mathématiques
que nous utilisons soient en fait un compromis entre ces deux
approches: intuitionniste puisqu'elles ont toujours su rendre
compte efficacement de la réalité physique, classique
puisqu'elles ont su s'affranchir du sens des axiomes dans la recherche
de théorèmes et qu'elles ont pris le parti d'englober
l'infini.
Les formules du calcul propositionnel
Il est temps de nous pencher sur certaines logiques
particulières, et ce de manière plus précise.
On s'intéresse la plupart du temps en logique à
des langages objets construits sous une forme générale,
celle du calcul propositionnel. Ce système fournit un cadre
général dans l'étude de langages objet plus
complexes. On peut visualiser le calcul propositionnel comme une
classe de langages possibles, ou comme un langage à part
entière. Il englobe la plupart des logiques connues et
utilisées en mathématiques.
On suppose tout d'abord qu'il existe des énoncés
primitifs que l'on appelle atomes, dont la structure interne,
ou le 'sens', nous est inconnue mais tels que l'on puisse différencier
deux énoncés distincts. Tous ces énoncés
sont représentés par une lettre de l'alphabet. Il
est important de souligner que le 'sens' des atomes est a
priori inconnu. Ce sont en fait des mots non définis.
On suppose de plus qu'il existe cinq procédés,
ou opérations, qui permettent de construire des
énoncés nouveaux à partir des énoncés
primitifs. On appelle ces énoncés nouveaux des formules
composées, atomes et formules composée constituant
les formules. Les cinq opérations sont " ",
"
",
" ", "
", "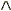 ",
"
",
" ", "
", "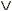 ".
Il est bien sûr possible de leur donner une interprétation
intuitive, mais dans le cadre de la logique ce n'est nullement
nécessaire. Conformément à ce que nous avons
dit plus haut, les mathématiques modernes s'affranchissent
du sens à accorder à ces signes (vocabulaire) pour
ne retenir que leur fonctionnement (grammaire). Ce n'est que lorsque
l'on se soucie d'interprétation physique que l'on se pose
la question du 'sens' à accorder à une formule.
Il est alors important de retrouver un sens intuitif aux cinq
opérations et aux termes primitifs, et c'est pourquoi nous
allons les exposer maintenant, tout en gardant à l'esprit
le fait que leur sens physique est hors du champ d'application
de la logique. "
".
Il est bien sûr possible de leur donner une interprétation
intuitive, mais dans le cadre de la logique ce n'est nullement
nécessaire. Conformément à ce que nous avons
dit plus haut, les mathématiques modernes s'affranchissent
du sens à accorder à ces signes (vocabulaire) pour
ne retenir que leur fonctionnement (grammaire). Ce n'est que lorsque
l'on se soucie d'interprétation physique que l'on se pose
la question du 'sens' à accorder à une formule.
Il est alors important de retrouver un sens intuitif aux cinq
opérations et aux termes primitifs, et c'est pourquoi nous
allons les exposer maintenant, tout en gardant à l'esprit
le fait que leur sens physique est hors du champ d'application
de la logique. " "
désigne l'équivalence, "
"
désigne l'équivalence, " "
l'implication, "
"
l'implication, "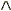 "
la conjonction ('et'), "
"
la conjonction ('et'), " "
la négation, et "
"
la négation, et "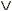 "
la disjonction ('ou'). L'emploi de parenthèses permet d'éviter
toute ambiguïté dans l'écriture de certaines
formules.
"
la disjonction ('ou'). L'emploi de parenthèses permet d'éviter
toute ambiguïté dans l'écriture de certaines
formules.
Exemple de proposition:
A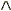 B
B B
B
que l'on peut traduire en Français par
ou encore, si l'on considère la table de
vérité de  (voir plus loin):
(voir plus loin):
- " Si A et B sont 'vrais', B est 'vrai' "
A chaque atome on accorde une valeur de vérité,
représenté par " VRAI " ou " FAUX ",
qui, là encore, peut être totalement arbitraire ou
être motivée par des raisonnements physiques. Des
schémas d'axiomes, ou, de manière équivalente,
des tables de vérité, nous décrivent comment
varie la valeur de vérité d'une formule en fonction
des atomes et des opérateurs qui la composent. A chaque
formule on peut donc associer une valeur logique VRAI ou FAUX,
sans toutefois que cela implique quoi que ce soit sur la 'vérité
physique' de la proposition. Des martiens pourraient parfaitement
utiliser le terme " VRAI " pour désigner
quelque chose qui n'est jamais vérifié et " FAUX "
pour le contraire, sans que cela bouleverse en quoi que ce soit
les résultats du calcul propositionnel. Remarquons que
VRAI et FAUX appartiennent au métalangage du calcul propositionnel,
ce sont des termes qui servent à 'parler' du calcul propositionnel.
Donnons un exemple de table de vérité,
avec la table de A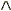 B
B B.
Cette table se présente comme un tableau, prenant en
entrée les valeurs de vérité possibles pour
A et B, et donnant en sortie les valeurs de vérité
de A
B.
Cette table se présente comme un tableau, prenant en
entrée les valeurs de vérité possibles pour
A et B, et donnant en sortie les valeurs de vérité
de A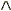 B
B B.
B.
|
B vrai |
B faux |
| A vrai |
A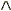 B B B vrai B vrai |
A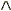 B B B vrai B vrai |
| A faux |
A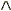 B B B vrai B vrai |
A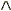 B B B vrai B vrai |
On constate que A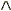 B
B B
est toujours vraie, même si A et B sont faux.
Ceci peut paraître déstabilisant et dur à
comprendre au premier abord, mais penser à 'l'équivalent'
français de cette phrase fait tout de suite disparaître
les difficultés: " si A et B alors B "
paraît en effet être une tautologie, donc toujours
vraie. Le fait que B soit faux ne change rien au fait que B implique
B !
B
est toujours vraie, même si A et B sont faux.
Ceci peut paraître déstabilisant et dur à
comprendre au premier abord, mais penser à 'l'équivalent'
français de cette phrase fait tout de suite disparaître
les difficultés: " si A et B alors B "
paraît en effet être une tautologie, donc toujours
vraie. Le fait que B soit faux ne change rien au fait que B implique
B !
Nous ne donnons pas ici les treize axiomes du calcul des propositions,
on pourra les retrouver sur le Web. Revenons juste rapidement
sur l'un d'entre eux, puisqu'il est à l'origine de la célèbre
loi du tiers exclu. Il s'agit du schéma d'axiomes n°11,
qui s'écrit, 
 A
A A
(en français: la double négation de A implique A).
La loi du tiers exclu telle que nous la connaissons est un théorème
du calcul des propositions, que l'on énonce comme suit:
A
A
(en français: la double négation de A implique A).
La loi du tiers exclu telle que nous la connaissons est un théorème
du calcul des propositions, que l'on énonce comme suit:
A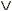 (
( A), en français:
" soit A est vrai soit la négation de A est vraie ".
Nous allons maintenant nous pencher sur une logique un peu plus
complexe, au sein du calcul propositionnel.
A), en français:
" soit A est vrai soit la négation de A est vraie ".
Nous allons maintenant nous pencher sur une logique un peu plus
complexe, au sein du calcul propositionnel.
Le calcul des prédicats et la notion de quantificateur
Ce calcul inclut le calcul propositionnel, mais y
ajoute deux opérations, "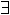 "
et "
"
et " ", qui 'signifient'
respectivement " il existe " et " quel
que soit ". Il s'agit là de quantificateurs.
Un quantificateur désigne généralement une
opération permettant de dire combien de fois on vérifie
une propriété au sein d'un ensemble. Ainsi "
", qui 'signifient'
respectivement " il existe " et " quel
que soit ". Il s'agit là de quantificateurs.
Un quantificateur désigne généralement une
opération permettant de dire combien de fois on vérifie
une propriété au sein d'un ensemble. Ainsi "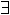 "
signifie que l'on vérifiera la propriété
une fois au moins, et "
"
signifie que l'on vérifiera la propriété
une fois au moins, et " "
que l'on retrouvera cette propriété pour tous les
éléments de l'ensemble. Il existe d'autres quantificateurs,
mais ceux ci sont les plus importants. Ces ajouts permettent de
rendre compte de la structure sujet-prédicat rencontrée
en grammaire courante. La majeure partie des inconvénients
que soulève cette structure 'primitive' dans le domaine
de la langue courante, pour reprendre les termes de Korzybski,
ne se retrouve pas en logique mathématique, puisque l'on
ne s'intéresse pas au contenu des phrases mais seulement
à la grammaire. Les limitations du modèle sujet-prédicat
sont ici d'ordre technique (on ne sait pas bien faire de la logique
autrement), et cette logique ne prétend pas rendre
compte parfaitement de la réalité.
"
que l'on retrouvera cette propriété pour tous les
éléments de l'ensemble. Il existe d'autres quantificateurs,
mais ceux ci sont les plus importants. Ces ajouts permettent de
rendre compte de la structure sujet-prédicat rencontrée
en grammaire courante. La majeure partie des inconvénients
que soulève cette structure 'primitive' dans le domaine
de la langue courante, pour reprendre les termes de Korzybski,
ne se retrouve pas en logique mathématique, puisque l'on
ne s'intéresse pas au contenu des phrases mais seulement
à la grammaire. Les limitations du modèle sujet-prédicat
sont ici d'ordre technique (on ne sait pas bien faire de la logique
autrement), et cette logique ne prétend pas rendre
compte parfaitement de la réalité.
En calcul des prédicats, nous supposons que
le langage objet contient des expressions pour des prédicats
à un nombre donné de variables, expressions
que l'on appelle expressions atomiques de prédicats.
Il s'agit en fait de phrases, de formules, dans un langage particulier,
contenant une partie variable qui peut prendre un certain nombre
de valeurs dans ce langage. La nature du langage objet sous-jacent
reste entièrement indéterminée: il peut s'agir
de formules mathématiques, d'anglais, etc. Les variables
utilisées dans les prédicats sont désignées
par des lettres minuscules. Les prédicats peuvent alors
être vus comme des formules composées, dont les
atomes sont variables. L'utilisation des quantificateurs permet
alors de se donner des schémas d'axiomes propres au calcul
des prédicats, axiomes qui vont permettre de décrire
comment se comportent les phrases en fonction des valeurs attribuées
aux variables. Nous ne nous étendrons pas plus sur ce calcul
plus compliqué que le calcul propositionnel, seuls les
concepts de base étant nécessaires à une
première approche de l'arithmétique formelle. Voici
les deux schémas d'axiomes du calcul des prédicats
sans égalité (i.e. sans l'utilisation du symbole
" = "), tels que l'on pourrait les retranscrire
en français:
- Si A(x) est vrai pour tout x,
il est vrai pour un z en particulier
- Si A(z) est vrai, alors il existe
une valeur de x pour laquelle A(x) est vraie
L'arithmétique formelle et la construction des entiers naturels
Il est temps maintenant d'arriver au but de notre
voyage: les fondements des mathématiques, les entiers naturels
et l'arithmétique formelle. L'arithmétique
'ordinaire' consiste à manipuler des nombres. On pourrait
penser que les opérations élémentaires que
vous avez apprises au cours élémentaire sont les
fondements de l'arithmétique, il est néanmoins possible
de les formaliser en utilisant le symbole ('), appelé
symbole successeur, dans le cadre du calcul propositionnel.
Nous reprenons les axiomes de Frankel sur la construction et l'existence
d'ensembles, et nous postulons l'existence d'un ensemble N qui
vérifie les postulats du calcul des prédicats et
du calcul propositionnel, et que l'on suppose non vide contenant
l'élément 0. On suppose de plus que l'on a rajouté
quelques 'mots' à notre vocabulaire, notamment le signe
('), le signe (+) (addition) et le signe (*)
(multiplication). Les signes nouveaux sont mis entre parenthèses
afin de bien les distinguer du corps du texte, notamment pour
le signe ('). On fait quelques suppositions supplémentaires
sur cet ensemble N, à l'aide d'axiomes dit mathématiques,
puisque ce sont des axiomes qui n'appartiennent pas à la
logique mathématique, mais qui permettent de décrire
efficacement et de manière intéressante l'ensemble
N.
Là encore, on trouvera ces axiomes sur le
Web. Ils énoncent le fonctionnement de l'addition et de
la multiplication, ainsi que quelques propriétés
essentielles de N: la relation successeur est injective (deux
nombres distincts ont un successeur distinct), 0 n'est le successeur
de personne, la propriété de récurrence,
etc.
Rappelons rapidement l'interprétation physique
du principe de récurrence: si une formule est vraie pour
0 et, si elle est vraie pour le successeur d'un entier dès
qu'elle est vraie pour cet entier, alors elle est vraie pour tous
les entiers naturels.
Ce système formel, et les axiomes qui l'accompagnent,
constitue, vous l'avez sans doute reconnu, l'ensemble des entiers
naturels, i.e. les nombres entiers. Cet ensemble a une importance
immense en mathématiques, puisque l'on peut dire, sans
trop se risquer, qu'il est à la base de 'toutes' les mathématiques
usuelles. Le simple fait de parler d'un nombre (relatif, réel,
rationnel, imaginaire, quaternion, etc.) présuppose l'existence
de ce système formel.
Un petit exemple amusant peut servir à illustrer
le caractère parfois trop 'contre-intuititif' de la démarche
formaliste. Le lecteur attentif du Web aura sans doute remarqué
l'absence d'axiome stipulant que a=a. Cette égalité
est bien vérifiée, mais il faut une démonstration
fastidieuse de 17 lignes pour y parvenir, en utilisant pas moins
de 7 axiomes ou schémas d'axiomes ! On peut toutefois
montrer que ce système formel est le plus petit qui contienne
toutes les propriétés de l'arithmétique 'ordinaire',
et c'est pourquoi on n'y rajoute pas d'axiomes supplémentaires,
même lorsque ceux-ci sont aussi évidents que a=a..
Le théorème de Gödel
Naturellement, les mathématiciens se sont
posé de nombreuses questions sur ce système formel
si important. Il faut rappeler que l'étude des propriétés
de N ne peut se faire que de 'l'extérieur' de N, avec ce
qu'on appelle la métamathématique. Le système
formel métamathématique comprend des notions nouvelles,
notamment la démontrabilité dans N. Une formule
de N est dite démontrable lorsqu'il existe une suite de
formules vraies, partant d'un ou plusieurs axiomes, reliées
entre elles par des schémas d'axiomes qui mènent
à la formule voulue. Une telle séquence de formules
est appelée démonstration.
La première question qui se pose alors est
la cohérence des axiomes: existe-t-il deux démonstrations,
l'une conduisant à une formule P, et l'autre à
la formule  P ? Si tel est
le cas, un résultat classique de logique nous dit que toute
formule du système formel est démontrable,
et le système est peu intéressant à étudier !
La cohérence des axiomes de N a été démontrée
rigoureusement, en métamathématiques, et ne pose
pas de problèmes. On a donc là un exemple d'une
proposition que la métamathématique parvient à
démontrer, donc qui est vraie dans un certain sens, et
qui n'est pas démontrable dans N, puisqu'il faut utiliser
un métalangage, sortir de N, pour le démontrer.
Cet exemple va conduire au célébrissime théorème
de Gödel, qui est probablement le théorème
'mathématique' qui a suscité le plus grand intérêt.
C'est également celui qui a fait dire le plus grand nombre
d'idioties. On peut l'énoncer comme suit (en français):
P ? Si tel est
le cas, un résultat classique de logique nous dit que toute
formule du système formel est démontrable,
et le système est peu intéressant à étudier !
La cohérence des axiomes de N a été démontrée
rigoureusement, en métamathématiques, et ne pose
pas de problèmes. On a donc là un exemple d'une
proposition que la métamathématique parvient à
démontrer, donc qui est vraie dans un certain sens, et
qui n'est pas démontrable dans N, puisqu'il faut utiliser
un métalangage, sortir de N, pour le démontrer.
Cet exemple va conduire au célébrissime théorème
de Gödel, qui est probablement le théorème
'mathématique' qui a suscité le plus grand intérêt.
C'est également celui qui a fait dire le plus grand nombre
d'idioties. On peut l'énoncer comme suit (en français):
Théorème d'incomplétude de Gödel:
Dans tout système axiomatique contenant
l'arithmétique formelle, il existe des propositions qu'on
ne peut ni démontrer, ni réfuter.
Il faut noter qu'en vertu de la loi du tiers exclu,
de telles propositions sont tout de même vraies ou fausses,
ce n'est que la capacité à démontrer cette
valeur de vérité qui est en jeu. On dit qu'une telle
proposition est indécidable. Il est amusant de remarquer
que, fondamentalement, le principe de la démonstration
de Godel est très proche du vieux paradoxe du menteur de
l'Antiquité: la proposition " Je ne suis pas
démontrable " est-elle démontrable ?
Tout l'art de Gödel a été de retranscrire cette
phrase dans le système formel adéquat et de la traiter
rigoureusement. Ce théorème fait désormais
partie de la réalité quotidienne des mathématiciens,
puisqu'on sait que de nombreuses propositions dans le système
axiomatique standard (système ZFC) sont indécidables.
Un rapide retour sur la loi du tiers exclu
Le calcul propositionnel présenté plus
haut, est la forme standard du calcul propositionnel. Il en existe
plusieurs variantes, notamment le calcul à trois valeurs
de vérité, et surtout le calcul propositionnel intuitionniste.
Dans ce calcul la loi du tiers exclu ( et le principe de double
négation), chère à Korzybski et Aristote,
ne sont ni valides ni démontrables. Korzybski refuse ce
vieil avatar de la logique aristotélicienne qu'est la loi
du tiers exclu, et explique que les mathématiques sont
le seul domaine dans lequel elle peut s'appliquer. En réalité,
il existe des mathématiques tout à fait consistantes
qui ont su s'affranchir de cette loi, mais ce sont des mathématiques
déconcertantes au premier abord. Le simple fait d'essayer
de les pratiquer permet de se rendre compte à quel point
la loi du tiers exclu est ancrée dans notre esprit et dans
nos prémisses.
En logique intuitionniste, l'axiome de double négation
est remplacé par l'axiome suivant:
 A
A (A
(A B).
Ce résultat particulier étant un théorème
du calcul standard, il apparaît clairement que le calcul
intuitionniste est un sous-ensemble du calcul standard: tous les
résultats de calcul intuitionniste sont vrais dans le calcul
standard, cependant il existe des résultats du calcul standard
qui ne sont pas vrais en calcul intuitionniste. Ce calcul est
très fructueux, et surtout présente l'avantage d'être
plus 'constructiviste'. Ceci signifie qu'il ne suffit pas
en général, pour démontrer l'existence d'un
objet, de montrer que sa non-existence conduit à une incohérence,
mais il faut au contraire exhiber l'objet dont on veut montrer
l'existence. La loi du tiers exclu, que l'on présente
souvent comme étant 'logique', n'est donc en fait que l'apanage
d'une logique spécifique, et n'est absolument pas inhérente
aux mathématiques. Il existe de nombreux édifices
mathématiques qui s'affranchissent de cette loi. Malgré
sa dénomination d'intuitionniste, insistons sur le fait
que l'utilisation de cette logique est très peu intuitive,
et que considérer que les notions de VRAI et de FAUX ne
s'opposent pas en logique, conduit à des résultats
parfois surprenants, et en tout cas toujours bizarres à
première vue. Nos anciennes prémisses sont encore
très actives !
B).
Ce résultat particulier étant un théorème
du calcul standard, il apparaît clairement que le calcul
intuitionniste est un sous-ensemble du calcul standard: tous les
résultats de calcul intuitionniste sont vrais dans le calcul
standard, cependant il existe des résultats du calcul standard
qui ne sont pas vrais en calcul intuitionniste. Ce calcul est
très fructueux, et surtout présente l'avantage d'être
plus 'constructiviste'. Ceci signifie qu'il ne suffit pas
en général, pour démontrer l'existence d'un
objet, de montrer que sa non-existence conduit à une incohérence,
mais il faut au contraire exhiber l'objet dont on veut montrer
l'existence. La loi du tiers exclu, que l'on présente
souvent comme étant 'logique', n'est donc en fait que l'apanage
d'une logique spécifique, et n'est absolument pas inhérente
aux mathématiques. Il existe de nombreux édifices
mathématiques qui s'affranchissent de cette loi. Malgré
sa dénomination d'intuitionniste, insistons sur le fait
que l'utilisation de cette logique est très peu intuitive,
et que considérer que les notions de VRAI et de FAUX ne
s'opposent pas en logique, conduit à des résultats
parfois surprenants, et en tout cas toujours bizarres à
première vue. Nos anciennes prémisses sont encore
très actives !
 ",
"
",
" ", "
", "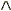 ",
"
",
" ", "
", "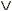 ".
Il est bien sûr possible de leur donner une interprétation
intuitive, mais dans le cadre de la logique ce n'est nullement
nécessaire. Conformément à ce que nous avons
dit plus haut, les mathématiques modernes s'affranchissent
du sens à accorder à ces signes (vocabulaire) pour
ne retenir que leur fonctionnement (grammaire). Ce n'est que lorsque
l'on se soucie d'interprétation physique que l'on se pose
la question du 'sens' à accorder à une formule.
Il est alors important de retrouver un sens intuitif aux cinq
opérations et aux termes primitifs, et c'est pourquoi nous
allons les exposer maintenant, tout en gardant à l'esprit
le fait que leur sens physique est hors du champ d'application
de la logique. "
".
Il est bien sûr possible de leur donner une interprétation
intuitive, mais dans le cadre de la logique ce n'est nullement
nécessaire. Conformément à ce que nous avons
dit plus haut, les mathématiques modernes s'affranchissent
du sens à accorder à ces signes (vocabulaire) pour
ne retenir que leur fonctionnement (grammaire). Ce n'est que lorsque
l'on se soucie d'interprétation physique que l'on se pose
la question du 'sens' à accorder à une formule.
Il est alors important de retrouver un sens intuitif aux cinq
opérations et aux termes primitifs, et c'est pourquoi nous
allons les exposer maintenant, tout en gardant à l'esprit
le fait que leur sens physique est hors du champ d'application
de la logique. " "
désigne l'équivalence, "
"
désigne l'équivalence, " "
l'implication, "
"
l'implication, "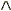 "
la conjonction ('et'), "
"
la conjonction ('et'), " "
la négation, et "
"
la négation, et "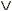 "
la disjonction ('ou'). L'emploi de parenthèses permet d'éviter
toute ambiguïté dans l'écriture de certaines
formules.
"
la disjonction ('ou'). L'emploi de parenthèses permet d'éviter
toute ambiguïté dans l'écriture de certaines
formules.
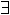 "
et "
"
et " ", qui 'signifient'
respectivement " il existe " et " quel
que soit ". Il s'agit là de quantificateurs.
Un quantificateur désigne généralement une
opération permettant de dire combien de fois on vérifie
une propriété au sein d'un ensemble. Ainsi "
", qui 'signifient'
respectivement " il existe " et " quel
que soit ". Il s'agit là de quantificateurs.
Un quantificateur désigne généralement une
opération permettant de dire combien de fois on vérifie
une propriété au sein d'un ensemble. Ainsi "